仓库重地，闲人免进

人是无用的激情。

——法国哲学家让·保罗·萨特《存在与虚无》

晨昏蒙影

老人与青年人，日出与日落，协调

关于博客的思考

1
date: 2021-09-15 15:47:32

博客是什么？

英文Weblog的音译，直译过来就是

Web(网络)+Log(日志)=网志。

也常被称为博客、部落格、部落阁、是一种在线日记型式的个人网站，借由张帖子章、图片或视频来记录生活、抒发情感或分享信息。来自wikipedia

用博客做什么？

博客可以记录生活，发表文章，做自媒体，商业推广...，我的定位是学习与生活的记录，用以提高写作技能，打字速度，以及表达，总结，记忆的能力。

该怎样经营博客？

一开始，我是把博客当作做笔记的平台，虽然现在也是如此，因为之前LaTeX\LaTeX玩得走火入魔，结果一写东西就搞得像写一本书似的，然后一边看资料一边在一个页面上修改来修改去，最后也没有收获，感觉就是定义与闲话的堆砌，如果它不能使我进步，反而拖累了生活，那我用它做甚。以后我就以章节或知识点的形式来写文章，学了一个阶段后，再统一总结起来。当然即兴的写作与每天的日记除外。

热情总会消减，有希望便有失望，心不死便不能复活。

逻辑学基本

时间：2021-09-18 23:10:49 描述：本文包含了逻辑学的一些定义与符号。

Not necessarily. This is a classic example of Munchhausen's Trilemma:

​ either the reason is predicated on a series of sub-reasons, leading to an infinite regression; or it tracks back to arbitrary axiomatic statements; or it's ultimately circular.

i.e., I'm moving out because I'm moving out.

-from 《The Big Bang Theory 2007》

前提&结论

(条件命题)一个命题都有前提和结论两部分，以若(前提)，则(结论)的形式表示。

条件

充分条件

充分条件前推后，若p，则q，亦即 p⇒qp\Rightarrow q

p⇒q(前项真，则后项真)¬p⇏¬q(前项非真，后项未知)p\Rightarrow q \quad \text{(前项真，则后项真)}\\ ¬p \nRightarrow ¬q\quad \text{(前项非真，后项未知)}\\

必要条件

必要条件后推前，若p发生,则q一定发生，亦即 p⇐qp\Leftarrow q

q⇏p(后项真，前项未知)¬q⇒¬p(后项非真，则前项非真)q \nRightarrow p\text{(后项真，前项未知)}\\ ¬q \Rightarrow ¬p\text{(后项非真，则前项非真)}\\

充要条件

充要条件两头推，亦即 p  ⟺  qp\iff q

常用的基本论证形式

名字 相继式 描述
肯定前件论式 (p ⇒ q) ; p ├ q 若 p 则 q；p ,所以 q
否定后件论式 (p ⇒ q) ; ¬q ├ ¬p 若 p 则 q；非 q；所以，非 p
假言三段论式 (p ⇒ q) ; (q ⇒ r) ├ (p ⇒ r) 若 p 则 q；若 q 则 r；所以，若 p 则 r
选言三段论式 (p ∨ q) ; ¬p ├ q 要么 p 要么 q；非 p；所以, q
创造性二难论式 (p ⇒ q)∧(r ⇒ s) ; (p ∨ r) ├ (q ∨ s) 若 p 则 q；并且若 r 则 s；但是要么 p 要么 r；所以，要么 q 要么 s
破坏性二难论式 (p ⇒ q)∧(r ⇒ s) ; (¬q ∨ ¬s) ├ (¬p ∨ ¬r) 若 p 则 q；并且若 r 则 s；但是要么非 q 要么非 s；所以，要么非 p 要么非 r
简化论式 (p ∧ q) ├ p p 与 q 为真；所以，p 为真
合取式 p, q ├ (p ∧ q) p 与 q 分别为真；所以，它们结合起来是真
增加论式 p ├ (p ∨ q) p 是真；所以析取式(p 或 q)为真
合成论式 (p ⇒ q) ∧ (p ⇒ r) ├ p ⇒ (q ∧ r) 若 p 则 q；并且若 p 则 r；所以，若 p 是真则 q 与 r 为真
德·摩根定律(1) ¬(p ∧ q) ├ (¬p ∨ ¬ q) (p 与 q)的否定等价于(非 p 或非 q)
德·摩根定律(2) ¬(p ∨ q) ├ (¬p ∧ ¬ q) (p 或 q)的否定等价于(非 p 与非 q)
交换律(1) (p ∨ q) ├ (q ∨ p) (p 或 q)等价于(q 或 p)
交换律(2) (p ∧ q) ├ (q ∧ p) (p 与 q)等价于(q 与 p)
结合律(1) p ∨ (q ∨ r) ├ (p ∨ q) ∨ r p 或(q 或 r)等价于(p 或 q)或 r
结合律(2) p ∧ (q ∧ r) ├ (p ∧ q) ∧ r p 与(q 与 r)等价于(p 与 q)与 r
分配律(1) p ∧ (q ∨ r) ├ (p ∧ q) ∨ (p ∧ r) p 与(q 或 r)等价于(p 与 q)或(p 与 r)
分配律(2) p ∨ (q ∧ r) ├ (p ∨ q) ∧ (p ∨ r) p 或(q 与 r)等价于(p 或 q)与(p 或 r)
双重否定律 p ├ ¬¬p p 等价于非 p 的否定
换位律 (p ⇒ q) ├ (¬q ⇒ ¬p) 若 p 则 q 等价于若非 q 则非 p
实质蕴涵律（蕴析律） (p ⇒ q) ├ (¬p ∨ q) 若 p 则 q 等价于要么非 p 要么 q
实质等价律(1) (p ↔ q) ├ (p ⇒ q) ∧ (q ⇒ p) (p 当且仅当q) 意味着，(若 p 是真则 q 是真)与(若 q 是真则 p 是真)
实质等价律(2) (p ↔ q) ├ (p ∧ q) ∨ (¬q ∧ ¬p) (p 当且仅当q) 意味着，要么(p 与 q 都是真)要么(p 和 q 都是假)
输出律 (p ∧ q) ⇒ r ├ p ⇒ (q ⇒ r) 从(如 p 与 q 是真则 r 是真)可推出(若 q 是真则 r 为真的条件是 p 为真)
输入律 p ⇒ (q ⇒ r) ├ (p ∧ q) ⇒ r 若p，则(q为真时，r为真)可推出若（p与q）为真，则r为真
重言式 p ├ (p ∨ p) p 是真等价于 p 是真或 p 是真
排中律 ├ (p ∨ ¬p) p 或非 p 是真
同一律* p = q ; p ⇒ r ├ q ⇒ r p = q 且 (若p 则 r )等价 (若q 则 r)
吸收律 p ⇒ q ├ p ⇒ (p ∧ q) 若p则q，可以推出若p则p且q

布尔运算

pdf

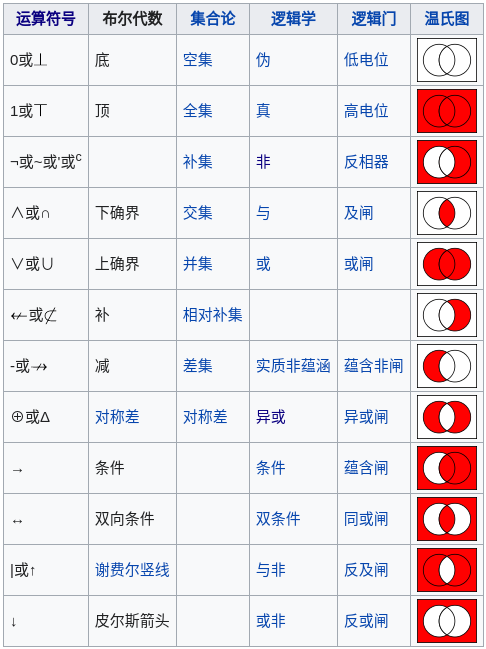
Boolean algebra

基本逻辑符号

符号 名字 解说 例子 读作
⇒→\rightarrow⊃ 实质蕴涵 A ⇒ B 意味着如果 A 为真，则 B 也为真；如果 A 为假，则对 B 没有任何影响。 x = 2 ⇒ x² = 4 为真，但 x² = 4 ⇒ x = 2 一般为假(因为 x 可以是 −2)。 蕴涵；如果.. 那么
⇔ ↔\Leftrightarrow\ \leftrightarrow 实质等价 A ⇔\Leftrightarrow B 意味着 A 为真如果 B 为真，和 A 为假如果 B 为假。 x + 5 = y +2 ⇔\Leftrightarrow x + 3 = y 当且仅当；
¬ ~/ 逻辑否定 陈述 ¬A 为真，当且仅当 A 为假。 ¬(¬A) ⇔\Leftrightarrow A x ≠ y ⇔\Leftrightarrow ¬(x = y) 非
∧ 逻辑合取 如果 A 与 B 二者都为真，则陈述 A ∧ B 为真；否则为假。 n < 4 ∧ n >2 ⇔\Leftrightarrow n = 3（当 n 是自 然数的时候）。 与；且
∨+ | 逻辑析取 如果 A 或 B有一个为真陈述 或二者均为真陈述，则 A ∨ B 为真；如果二者都为假，则 陈述为假。 n $ \ge$ 4 ∨ n≤\le 2 ⇔\Leftrightarrow n ≠ 3（当 n 是 自然数的时候）。 或
⊕⊻ XORXOR 陈述 A ⊕ B 为真，在要么 A 要么 B 但不是二者为真的时候为真。A ⊻ B 意思相同。 (¬A) ⊕ A 总是真，A ⊕ A 总是假。 异或
∀ 全称量词 ∀ x: P(x) 意味着所有的 x 都使 P(x) 都为真。 ∀ n ∈ N : n² ≥\gen 对于所有
∃ 存在量词 ∃ x: P(x) 意味着有至少一个 x 使 P(x) 为真。 ∃ n ∈ N（n 是偶数）。 存在着
∃! 唯一量词 ∃! x: P(x) 意味着精确的有一个 x 使 P(x) 为真。 ∃! n ∈ N（n + 5 = 2n）. 精确的存在一个
:= ≡ 定义 x := y 或 x ≡ y 意味着 x 被定义为 y 的另一个名字(但要注意 ≡ 也可以意味着其他东西，比如全等)。 cosh x := (1/2)(exp x + exp (−x)) 被定义为
:⇔\Leftrightarrow P :⇔\Leftrightarrow Q 意味着 P 被定义为逻辑等价于 Q。 A XOR B :⇔\Leftrightarrow (A ∨ B) ∧ ¬(A ∧ B)
( ) 优先组合 优先进行括号内的运算。 (8/4)/2 = 2/2 = 1, 而 8/(4/2) = 8/2 = 4。
├ 推论 x ├ y 意味着 y 推导自 x。 A → B ├ ¬B → ¬A 推论或推导
□\Box L 必然性 □P{\displaystyle \Box P}意味着如果P{\displaystyle P}不可能，为假。 ◊p=¬ □ ¬ p\Diamond p=\lnot \,\Box \,\lnot \,p 必然的
◊\Diamond M 可能性 ◊P\Diamond P意味着如果P{\displaystyle P}可能为真，不管实际上是真是假。 □p=¬ ◊ ¬ p\Box p=\lnot \,\Diamond \,\lnot \,p 可能的

参考

Conway's Game of Life

时间：2021-09-22 09:59:15 描述：生命游戏的基本介绍

康威生命游戏（英语：Conway's Game of Life），又称康威生命棋，是英国数学家约翰·何顿·康威在1970年发明的细胞自动机。

生命游戏是一个零玩家游戏。它包括一个二维矩形世界，这个世界中的每个方格居住着一个活着的或死了的细胞。一个细胞在下一个时刻生死取决于相邻八个方格中活着的或死了的细胞的数量。如果相邻方格活着的细胞数量过多，这个细胞会因为资源匮乏而在下一个时刻死去；相反，如果周围活细胞过少，这个细胞会因太孤单而死去。实际中，玩家可以设定周围活细胞的数目怎样时才适宜该细胞的生存。如果这个数目设定过高，世界中的大部分细胞会因为找不到太多的活的邻居而死去，直到整个世界都没有生命；如果这个数目设定过低，世界中又会被生命充满而没有什么变化。

实际中，这个数目一般选取2或者3；这样整个生命世界才不至于太过荒凉或拥挤，而是一种动态的平衡。这样的话，游戏的规则就是：当一个方格周围有2或3个活细胞时，方格中的活细胞在下一个时刻继续存活；即使这个时刻方格中没有活细胞，在下一个时刻也会“诞生”活细胞。

在这个游戏中，还可以设定一些更加复杂的规则，例如当前方格的状况不仅由父一代决定，而且还考虑祖父一代的情况。玩家还可以作为这个世界的“上帝”，随意设定某个方格细胞的死活，以观察对世界的影响。

在游戏的进行中，杂乱无序的细胞会逐渐演化出各种精致、有形的结构；这些结构往往有很好的对称性，而且每一代都在变化形状。一些形状已经锁定，不会逐代变化。有时，一些已经成形的结构会因为一些无序细胞的“入侵”而被破坏。但是形状和秩序经常能从杂乱中产生出来。

规则

生命游戏中，对于任意细胞，规则如下：

  • 每个细胞有两种状态 - 存活或死亡，每个细胞与以自身为中心的周围八格细胞产生互动。
  • 当前细胞为存活状态时，当周围的存活细胞低于2个时（不包含2个），该细胞变成死亡状态。（模拟生命数量稀少）
  • 当前细胞为存活状态时，当周围有2个或3个存活细胞时，该细胞保持原样。
  • 当前细胞为存活状态时，当周围有超过3个存活细胞时，该细胞变成死亡状态。（模拟生命数量过多）
  • 当前细胞为死亡状态时，当周围有3个存活细胞时，该细胞变成存活状态。（模拟繁殖）
  • 可以把最初的细胞结构定义为种子，当所有在种子中的细胞同时被以上规则处理后，可以得到第一代细胞图。按规则继续处理当前的细胞图，可以得到下一代的细胞图，周而复始。

更详细的介绍玩法可以看这个WIKI：Tutorials - LifeWiki (conwaylife.com)

在线模拟器

大家可以在下面进行模拟，右键添加，中建缩放。

安卓模拟器

Game of Life (康威生命游戏模拟)

其实，我的目的是要把这个软件卸载掉，但又担心以后找不到了，就凑了一篇“祭文”。

人的底层逻辑

此文是读了《社会心理学》之后想写，但是自身储备不足，导致烂尾，怎么也续不上了。等到以后有经历了，有体会了，再来完善之。

1
2
3
4
5
6
abbrlink: Meta-Logic4Human-mind
categories:
  - 生活
  - "\U0001F3AD人的底层逻辑"
date: 2023-02-28 12:48:18
update: 2023-02-28 12:48:18

社会心理学

人，生而局限。

——秉蕳

文章痕迹

  • 2023-02-28 听《907经典留声》中对《孙子兵法》与《狂飙》的分析有所感触，又结合这两天读的《社会心理学》、《密码简史》中对象的分析，觉得有必要专门开设个分类来对人性、心理学、历史进行研读，以得到如何做人的初步认识，然后再以此指导未来的经历，最后反过来完善对于人的认识。
  • 2023-03-05 本文为书中第二部分的笔记总结：群体，吸引，关系，社会自我
  • 2023-03-05 从未有无瑕的白玉，从未有面面俱到的文章，本系列文章将从笔者有体会的几个方面进行探讨，而不是把全文照抄过来。经过考量，人与环境本身就是不可分割的，本文的主题将保持为《人的底层逻辑》，不再割裂出《人性塑造工程》部分。

简介

本页是《人的底层逻辑》系列笔记、文章的汇总页。由许多篇小文整合而成。

学习了《马克思主义》后，我发觉用它来解释哲学与人类发展的规律很不错，甚至对于那些怪乎其邪的宗教也具有很强的解释能力，用数学的语言来说，这就是一个普适性很强的模型。那么对于心理学这个方面，就用《吉洛维奇社会心理学》来构建这个模型，希望完成这个计划之后可以用这个模型来解释七八成的现象。 ——田欣洋

社会助长——他人存在对自身行为的影响

仅仅意识到他人的存在就会影响自身的表现。

“另一个骑手的存在是对骑手的一种刺激，它激起了骑手竞争的本能；另一个人的存在也可以作为放松或释放紧张情绪的方式，这是自己无法做到的。”

——诺曼·特里普利特(Norman Triplett)

人性塑造工程

知行合一只是一种幻想。

——Sion

读社会心理学第八章有感触，遂想写此文，本文为书中第六七八章的总结：社会影响，态度与劝导，态度与行为。

很多年轻人对自己被强迫去教堂、寺庙或清真寺感到恼火，他们总是抱怨：“为什么我要去那？我一点都不相信这些东西。”但是，他们中的很多人却被告知：“你相不相信这些东西并不重要，重要的是你继续参与学习和祷告。”对此，一些年轻人会反抗到底，一旦他们的父母允许便立即抛开这些东西。但相当多的另一部分年轻人则会坚持下去，在继续参与这些活动之后，他们发现自己开始真诚地相信某些宗教信条了，而这些信条正是他们原先所抵触的。随着时间推移，纯粹的外显行为开始给真诚的内在信仰让路。

我起初抵触中国传统上的道教佛教，但是看了一些书后，观念就改变了许多，八卦并不封建，只是对世界的一种解读而已，就跟原子电子模型一样，没必要产生那么大的偏见。为了庆祝我思想的转变，咱家买了个八卦装饰的怀表(鬼魅速去！吾赛博道士是也！)。

姑息关怀

这是读了英语世界一期杂志后引发的冲动，是“💀死亡”分类下的第一篇文章，但是体会太少[1]（唯一的亲人离世还是8岁时的老奶）

1
2
3
title: 姑息关怀
date: 2023-04-28 08:57:38
update: 2023-04-28 08:57:38

  1. 我写着句话简直就是在招母亲骂，但是既然写了就不要害怕，所有的事情与这篇文章绝对毫无关系！ ↩︎