晶体结构与几何理论

前言
晶体(crystal)大多数有规则的多面体外形,但并不是所有的晶体都有固定的外形,比如金属、雪花❄、单晶硅等,都没有固定外形。
晶体的性质
在一般情况下,单晶体(非立方晶系)的许多宏观物理量都具有各向异性,而非晶体或者立方晶系都具有各向同性。但由细微单晶体组成的多晶体,有些特殊,在一般情况下,它表现为各向同性,在外界环境(电磁场、力场等)作用下会变现为各向异性,最简单的例子就是磁铁🧲了,究其原因,就是这些细微的单晶体在外界作用下进行了择优取向,从而使整个多晶体表现为了各向异性。
晶体结构
不同材料的非结晶陶瓷通常透明🔎,相同材料的晶体倾向于不透明🗿。
基本概念
晶体:在较大原子范围内,原子进行周期重复性排列(长程有序)
非晶体:是其中的原子不按照一定空间顺序排列的固体,与晶体相对应。
晶体具有确定的熔沸点,各向异性;非晶体没有确定熔沸点,各向同性。
晶胞:将结构分为许多小的重复单元(基本结构单元,棱角与中心原子一致)
晶体结构:原子、分子、离子在空间排列的方式。
金属晶体结构
定义
配位数:晶格中与某一原子相距最近的原子个数。
致密度(APF):
面心立方晶体结构(Face Center Cubic)
-
金属:γ铁(γ-Fe)、钙(Ca)、锶(Sr)、铝(Al)、铜(Cu)、银(Ag)、金(Au)、镍(Ni)、钯(Pd)、铂(Pt)、铑(Rh)、铱(Ir)、铅(Pb)
-
晶胞原子数:4
-
配位数:12
-
致密度:0.740480489
-
原子半径:
体心立方晶体结构(Body Center Cubic)
-
金属;碱金属,a铁,难熔金属(钒(V)、铌(Nb)、钽(Ta)、铬(Cr)、钼(Mo)、钨(W))
-
晶胞原子数:2
-
配位数:8
-
致密度:0.68017476158
-
原子半径:
密排六方晶体结构(Hexagonal Close Packed)
- 金属:镁(Mg)、铍(Be)、钴(Co)、锌(Zn)、镉(Cd)、铊(Tl)和3族元素钪(Sc)、钇(Y)、4族元素钛(Ti)、锆(Zr)、铪(Hf)、镧系元素等
- 晶胞原子数:6
- 配位数:12
- 致密度:0.740480489
- 原子半径:
金属固体可以通过下面的公式计算理论密度:
其中n为每个晶胞中原子的数目,A为原子量,为晶胞的体积,
陶瓷晶体结构
晶系
为了准确地表示3维空间的晶体结构,引入晶格参数:长宽高分别用晶格常数表示,夹角用表示,可以利用晶格参数计算晶体的体积:
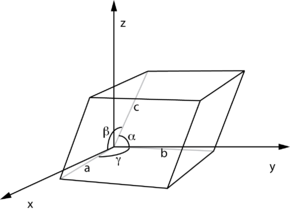
各种晶格结构又可以归纳为七大晶系:
| 晶系 | 布拉维格子 |
|---|---|
| 三斜晶系 | 简单三斜 |
| 单斜晶系 | 简单单斜 底心单斜 |
| 斜方晶系 | 简单正交 底心正交 体心正交 面心正交 |
| 三方晶系 | 三方 |
| 四方晶系 | 简单四方 体心四方 |
| 六方晶系 | 六方 |
| 立方晶系 | 简单立方 体心立方 面心立方 |
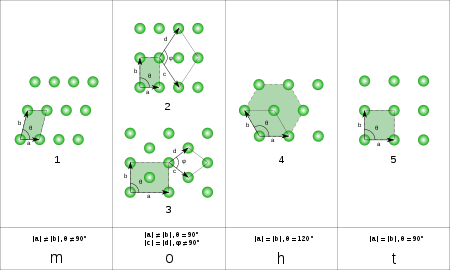
二维情形
布拉维晶格在二维平面上有五种类型,两晶轴,夹角,分为斜晶格,正方形晶格,六边形晶格,矩形晶格,中心矩形晶格,如图所示:
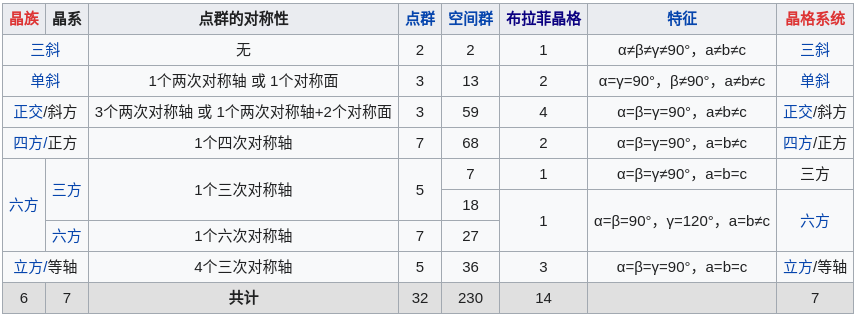
各种晶系分别与十四种空间格(称作布拉维晶格)相对应,对应表如下:
文字不够吗?来看图吧:
关于各种化合物的三维结构图参见日文的晶体结构维基,写的真不赖。
点坐标
晶向与晶面
线密度与面密度
固体缺陷(crystalline imperfection)
具有完整的点阵结构的晶体是理想化的,称为 理想晶体。
理想晶体在自然界中是不存在的。在任何一个实际 晶体中,原子、分子、离子等的排列总是或多或少地与理想点阵结构有所偏离。那些偏离理想点阵结构的部位称作晶体的缺陷或者晶体的不完整部位。
点缺陷
肖托基空位




