生命的最大用处时将其用在更长久的地方上
——威廉·詹姆斯
为了更好的阅读,请点击“阅读模式”按钮。
引言
先理一下积分区域与各个积分之间的关系:
| 积分区域 |
积分学 |
| 直线区间 |
定积分 |
| 平面区域 |
二重积分 |
| 空间区域 |
三重积分 |
| 曲线弧段 |
曲线积分 |
| 曲面区域 |
曲面积分 |
在不同区域内做的积分,各不相同却又相互联系。
曲线积分
用物理学来理解的话,就是求一个细长线的质量,如果密度为一的话,那就是线的长度了
对弧长的曲线积分
(第一类曲线积分)
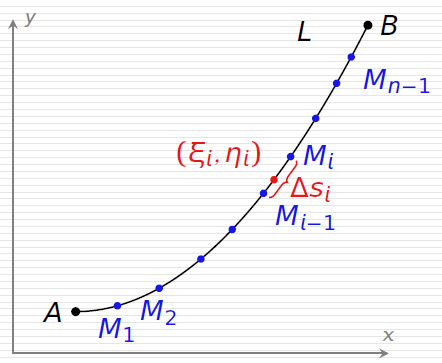
条件是:L光滑,f(x,y)有界,点在线上。如图,定义曲线积分为:
∫Lf(x,y)ds=λ→0limi=1∑nf(ξi,ηi)Δsi
L称为积分弧段,ds称为弧长元素,当曲线封闭时这样写:∮f(x,y)ds
性质
- 线性和
∫L(αf+βg)ds=α∫Lfds+β∫Lgds
- 分段和
∫Lf(x,y)ds=∫L1f(x,y)ds+∫L2f(x,y)ds
- 保号性
∫Lf(x,y)ds≥∫Lg(x,y)ds{f(x,y)≥g(x,y)}
- 对称性
曲线关于y轴对称,函数关于x为奇函数,值为零,偶函数,值倍之。
关于x轴对称,…
计算法
参数方程:用一个独立变量的函数来表示xyz等变量,组成的方程称为参数方程。
定义法
设平面曲线 L 的参数方程为 {x=ϕ(t)y=ψ(t), 其 中 a⩽t⩽b, 则弧长元素ds=ϕ′(t)2+ψ′(t)2dt,得到计算公式:
∫Lf(x,y)ds=∫abf(ϕ(t),ψ(t))ϕ′(t)2+ψ′(t)2dt
对于三维情形⎩⎪⎨⎪⎧x=ϕ(t)y=ψ(t)(a≤t≤b)z=ζ(t) 则有:
∫Lf(x,y,z)ds=∫abf(ϕ(t),ψ(t),ζ(t))ϕ′(t)2+ψ′(t)2+ζ′(t)2dt
特殊情况:
- 当曲线方程为 y=ψ(x) (a≤x≤b)时有:
∫Lf(x,y)ds=∫abf[x,ψ(x)]1+ψ′(x)2dx
- 当曲线方程为 x=ϕ(y) (a≤y≤b)时有:
∫Lf(x,y)ds=∫abf[ϕ(y),y]ϕ′(y)2+1dy
对坐标的曲线积分
(第二类曲线积分)
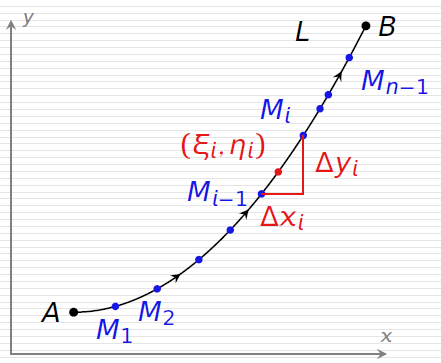
可以类比为力沿着曲线做功,条件就是曲线光滑,有界,点在线上,分别沿x轴与沿着y轴进行积分,可以得到两个公式:
∫LP(x,y)dx=λ→0limi=1∑nP(ξi,ηi)Δxi∫LP(x,y)dy=λ→0limi=1∑nP(ξi,ηi)Δyi
性质
- (线性和) 设 α 和 β 为常数, 则
∫L(αP1+βP2)dx=α∫LP1dx+β∫LP2dx
- (分段和) 将有向曲线弧 L 分成 L1 和 L2, 则
∫LP(x,y)dx=∫L1P(x,y)dx+∫L2P(x,y)dx
- (方向性)设L−1是L的反向曲线弧,则
∫L−P(x,y)dx=−∫LP(x,y)dx
计算法
跟第一类的相似,不同的是t有了方向(单调)性(a→b),此时dx=ϕ′(t)dt, dy=ψ′(t)dt。
∫LP(x,y)dx+Q(x,y)dy=∫ab[P(ϕ(t),ψ(t))ϕ′(t)+Q(ϕ(t),ψ(t))ψ′(t)]dt
特殊情况:当 y=ψx,(x:a→b)则
∫LP(x,y)dx+Q(x,y)dy=∫ab[P(x,ψ(x))+Q(x,ψ(x))ψ′(x)]dx
🔗两类曲线积分之间的联系
设有向曲线弧 L 的参数方程为x=ϕ(t),y=ψ(t),t 从 a 到 b,a<b,则有:
==∫LPdx+Qdy=∫ab[Pϕ′(t)+Qψ′(t)]dt∫ab[ϕ′2+ψ′2P⋅ϕ′+ϕ′2+ψ′2Qψ′]⋅ϕ′2+ψ′2dt∫L(Pcosα+Qcosβ)ds
格林公式
∬D(∂x∂Q−∂y∂P)dxdy=∫LPdx+Qdy
即:在平面闭区域D上的二重积分可以通过沿闭区域D的边界曲线L 上的曲线积分来表达.利用这个公式也可以计算闭区域D的面积。
**定理:**设 G 是单连通区域, 函数 P(x,y),Q(x,y) 在 G 内具有一阶连续偏导数, 则下述等价:
- 在 G 内的曲线积分 ∫LPdx+Qdy 与路径无关。
- 在 G 内的闭曲线积分 ∮CPdx+Qdy 恒为零。
- 在 G 内 ∂x∂Q=∂y∂P 恒成立。
- 在 G 内存在 u(x,y), 使得 du=Pdx+Qdy。
曲面积分
还用物理学来理解的话,就是求一个无限薄的板的质量,如果面密度为一的话,那就是板的面积了
对面积的曲面积分
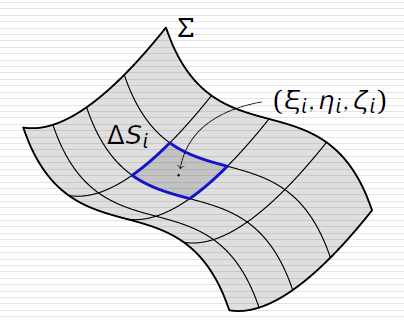
定义 f(x,y,z) 在 Σ 上对面积的曲面积分
∬Σf(x,y,z)dS=λ→0limi=1∑nf(ξi,ηi,ζi)ΔSi
其中 ∑ 称为积分曲面, dS 称为面积元素.
性质
- 线性和
∬∑(αf+βg) dS=α∬∑f dS+β∬∑g dS
- 分片和
∬∑f dS=∬∑1f dS+∬∑2f dS
- 保号性
∬∑f(x,y,z) dS≥∬∑g(x,y,z) dS{f(x,y,z)≥g(x,y,z)}
- 对称性
曲面关于xOy面对称,函数关于z为奇函数,值为零,偶函数,值倍之。
关于x轴对称,…
计算法
设曲面 Σ 的方程为 z=z(x,y), 它在 xOy 面的投影 区域为 Dxy. 则对曲面的面积积分可以化为二重积分:
=∬Σf(x,y,z)dS∬Dxyf(x,y,z(x,y))1+zx2(x,y)+zy2(x,y)dxdy
对坐标的曲面积分
∬ΣPdydz+∬ΣQdzdx+∬ΣRdxdy
🔗两类曲面积分之间的联系
∬ΣPdydz+Qdzdx+Rdxdy=∬Σ(Pcosα+Qcosβ+Rcosγ)dS
高斯公式
设空间闭区域 Ω 是由分片光滑 的闭曲面 ∑ 所围成, 函数 P(x,y,z),Q(x,y,z,, 和 R(x,y,z) 在 Ω 上具有一阶连续偏导数, 则有
∭Ω(∂x∂P+∂y∂Q+∂z∂R)dv=∬ΣPdydz+Qdzdx+Rdxdy=∬Σ(Pcosα+Qcosβ+Rcosγ)dS
其中有向曲面 Σ 是 Ω 的整个边界曲面的外侧.



