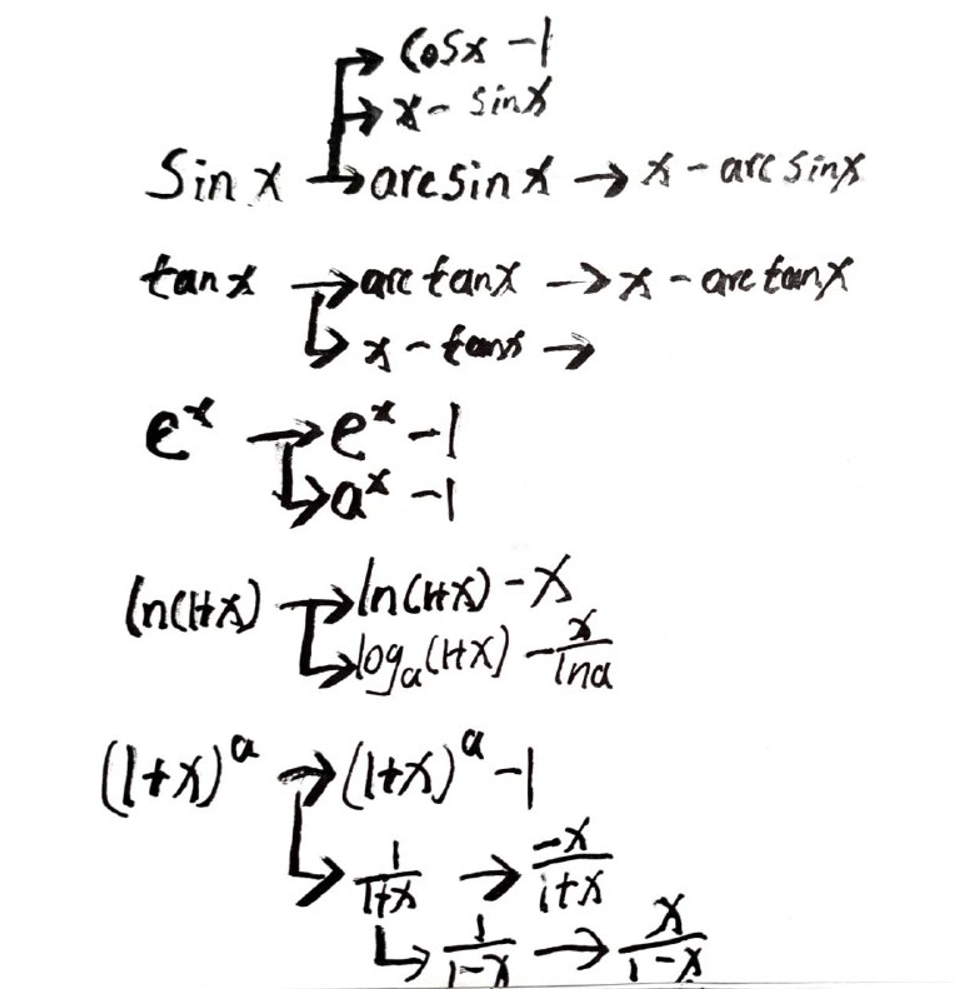泰山之管穿石,单极之绠断干。水非石之钻,索非木之锯,渐靡使之然也。
——东汉·班固《汉书·枚乘传》
楔子
前两天看到 blackpenredpen曹老师 的视频,有感触,觉得对于数学的学习而言,刷题中才能真正学会东西。有些东西,看了不一定理解,理解了不一定会应用,用了不一定真正掌握。做题能很好的杂糅这一切,让理解更深入,记忆更加清晰。
收集到22个,感觉没得写了。早上偶然看到mdnice群里有人发导数的笔记,然后又翻到了他之前的极限笔记。然而,笔记里第一题我都做的吃力,NND,再看才知晓是Wu老的高数17天。然后找来翻了翻,光极限就讲了57页😮,当然里面方法还是基本方法,但很多都是“稍稍”延伸了几步,却足以让我手足无措。这两天不能放松,好好理理思路。
利用泰勒展开式推导出所有常见无穷小(4 → 50)
初出茅庐
这一部分有27道例题,主要介绍极限计算的基本方法。
\begin{equation}
\lim_{n\to \infty}\ \frac{1}{\sqrt{n^2+1}}+\frac{1}{\sqrt{n^2+2}}+\dots \frac{1}{\sqrt{n^2+n}}
\end{equation}
bg
提示:利用夹逼定理(🗣️哪—里—跑—)
n2+11∗n≤bn≤n2+n1∗n
\begin{equation}
\lim _{x \rightarrow 0} \frac{\ln \left(1+4 x^{2}\right)}{\sin x^{2}}
\end{equation}
Answer
提示:等价无穷小
sin(🥕)∼ln(1+🥕)
x→0limsinx2ln(1+4x2)=x24x2= 4
\begin{equation}
\lim_{x \rightarrow 0} x^{3} \sin \frac{1}{x^{3}}
\end{equation}
bg
提示:注意等价无穷小的条件
x3为无穷小,∣sinx31∣≤1无穷小与有界变量的乘积仍为无穷小∴x→0limx3sinx31=0
\begin{equation}
\lim_{x \rightarrow 0} \frac{\sin x-\tan x}{x^{3}}
\end{equation}
bg
提示:拼凑等价无穷小
limx→0x3sinx−tanx=x→0limx3sinx(1−cosx1)=x→0limx3cosxsinx(cosx−1)=x→0limx3x⋅(−21x2)=−21
\begin{equation}
\lim _{x \rightarrow 0}\left(1+x e^{x}\right)^{\frac{1}{x}}
\end{equation}
bg
提示:1∞常规思路·第一弹
x→0lim(1+🥕)🥕1=e(🥕=0)
\begin{equation}
\lim _{x \rightarrow 0}\left(\frac{1-\tan x}{1+\tan x}\right)^{\frac{1}{-\sin 2 x}}
\end{equation}
bg
提示:1∞常规思路·第二弹
x→0lim(1+tanx1−tanx)−sin2x1=x→0lim(1+(1+tanx1−tanx−1))1+tanx1−tanx−11×1+tanx−2tanx−sin2x1=x→0lime1+tanx−2tanx−sin2x1=x→0lime1+tanx−2x−2x1=x→0lime1+tanx1=e
\begin{equation}
\lim_{n\to \infty} (\sqrt{n^2+n}-n)
\end{equation}
bg
提示:常规思路:平方差拼凑
n→∞lim(n2+n−n)=n→∞lim(1n2+n−n)=n→∞lim(n2+n+n)n2+n−n2=n→∞lim(n2+n+n)n=n→∞lim(1+n1+11)=21
\begin{equation}
\lim_{x\to \infty} \sqrt{x}(\sqrt{x+2}-\sqrt{x-3})
\end{equation}
bg
提示:常规思路:平方差拼凑
x→∞limx(x+2−x−3)=x→∞lim1x(x+2−x−3)=x→∞limx+2+x−3)x×5=x→∞lim1+2/x+1−3/x)5=25
\begin{equation}
\lim _{x \rightarrow 0}\left(\frac{1}{x}-\frac{1}{e^{x}-1}\right)
\end{equation}
bg
提示:凑乘积形式,等价无穷小+洛必达
x→0lim(x1−ex−11)=x→0lim((ex−1)xex−1−x)=x→0lim(x2ex−1−x)=x→0lim(2xex−1)=x→0lim(2ex)=21
\begin{equation}
\lim_{x\to 0} \frac{(x-\sin x) e^{-x^2}}{\sqrt{1-x^3}-1}
\end{equation}
bg
提示:等价无穷小替换
(1+🥕)a−1∼a🥕
x→0lim1−x3−1(x−sinx)e−x2=x→0lime−x2×x→0lim1/2×(−x3)x−sinx=−2×x→0limx3x−sinx洛必达法则=−2×x→0lim3x21−cosx=−2×x→0lim3x21/2×x2=−31
\begin{equation}
\lim_{x\to 0} \frac{x-\sin 2x}{x + \sin 5x}
\end{equation}
bg
提示:加减法使用等价无穷小的条件
∵ 当 x→0 时, sin2x∼2x,sin5x∼5x, 且 limx→0xsin2x =2=1,limx→0xsin5x=5=−1,
满足等价无穷小替换对加减法成立的条件,
∴x→0limx+sin5xx−sin2x=x→0limx+5xx−2x=−61
\begin{equation}
\lim _{x \rightarrow \infty}\left(\cos \frac{1}{x}\right)^{x^{2}}
\end{equation}
bg
提示:1∞型·第三弹
x→∞lim(cosx1)x2=x→∞lim[1+(cosx1−1)]cosx1−11×(cosx1−1)×x2=ex→∞lim(cosx1−1)x2=ex→∞lim(x1)2cosx1−1=ex→∞lim(−x1)2−21(x1)2=e−21=e1
\begin{equation}
\lim _{x \rightarrow \infty} \frac{(x+a)^{x+a}(x+b)^{x+b}}{(x+a+b)^{2 x+a+b}}
\end{equation}
bg
提示:1∞型·第四弹
x→∞lim(x+a+b)2x+a+b(x+a)x+a(x+b)x+b=x→∞lim(x+a+b)x+a(x+a)x+a⋅(x+a+b)x+b(x+b)x+b=x→∞lim(1+x+ab)x+a1⋅(1+x+ba)x+b1=eb1⋅ea1=e−(a+b)
\begin{equation}
\lim _{x \rightarrow 0}\left[\frac{\ln (x+\sqrt{1+x^{2}})}{x}\right]^{\frac{1}{1-\cos x}}
\end{equation}
bg
提示:1∞型·第五弹,常规思路
幂化简:原式x→0lim[xln(x+1+x2)]1−cosx1=x→0lim[1+xln(x+1+x2)−x]1−cosx1=x→0limex(1−cosx)ln(x+1+x2)−xx→0limx⋅21x2ln(x+1+x2)−x=x→0lim23x21+x21−1=x→0lim23x2−21x2=−31=e−31
\begin{equation}
\lim _{n \rightarrow \infty}\left(\frac{\pi}{2}-\arctan n\right)^{\frac{1}{\ln n}}
\end{equation}
bg
提示:1∞型·变体,思路还是一样的,幂运算变乘法
幂化简:原式n→∞lim(2π−arctann)lnn1=n→∞limelnxln(π/2−arctanx)n→∞limlnxln(π/2−arctanx)=x→+∞limx12π−arctanx1⋅(−1+x21)=−x→+∞lim2π−arctanxx1=−x→+∞lim−1+x21−x21=−1=e−1
\begin{equation}
\lim_{x\to 0} \frac{1-\cos^2x-\frac{1}{2} x \sin 2x}{x^2(e^{x^2}-1)}
\end{equation}
bg
提示:多次使用洛必达法则
x→0limx2(ex2−1)1−cos2x−21xsin2x=x→0limx2×x21−cos2x−21xsin2x上下都趋近于0,使用洛必达法则=x→0lim4x32cosxsinx−21sin2x−cos2x×x=x→0lim4x321sin2x−cos2x×x上下都趋近于0,使用洛必达法则=x→0lim12x2cos2x−cos2x+sin2x×2x=x→0lim12x22x×2x=31
\begin{equation}
\lim _{x\to 0}(\frac{1}{x^2}-\frac{1}{\sin^2x})
\end{equation}
bg
提示:多次使用洛必达法则
x→0lim(x21−sin2x1)=x→0limx2sin2xsin2x−x2上下都趋近于0,使用洛必达法则=x→0lim4x3sin2x−2x上下都趋近于0,使用洛必达法则=x→0lim12x22cos2x−2=x→0lim6x2cos2x−1=x→0lim6x221(2x)2=31
\begin{equation}
\lim _{x \rightarrow 0} (\frac{\cos x}{\cos 2x})^{\frac{1}{x^2}}
\end{equation}
bg
提示:等价无穷小之 加不反
x→0lim(cos2xcosx)x21=ex→0limx2(cos2xcosx−1)=ex→0limx2cos2xcosx−cos2x=ex→0limx2cosx−cos2x=ex→0lim2x−sinx+2sin2x∵x→0lim2sin2x−sinx=−1=e23
\begin{equation}
\lim _{x \rightarrow 0} \frac{[\sin x-\sin (\sin x)] \cdot \sin x}{x^{4}}
\end{equation}
bg
提示:等价无穷小+洛必达法则
x→0limx4[sinx−sin(sinx)]⋅sinx=x→0lim3x2cosx−cos(sinx)⋅cosx=x→0limcosx×x→0lim3x21−cos(sinx)=x→0lim3x221sin2x=x→0lim6x21x2=61
\begin{equation}
\text{求正的常数a与b,使下式成立:}
\lim _{x \rightarrow 0} \frac{1}{b x-\sin x} \int_{0}^{x} \frac{t^{2}}{\sqrt{a+t^{2}}} d t=1
\end{equation}
bg
提示:洛必达+等价无穷小,看见积分,必定洛必达。
x→0limbx−sinx1∫0xa+t2t2dtx→0limb−cosxa+x2x2x→0lima+x21×x→0limb−cosxx2a1×x→0limb−cosxx2a1×x→0limb11−b1cosxx2a1×x→0limb12b1x2−b1+1x2a1×2a(a=4→🥝)⟹b=1=1=1=1🥝=1=1=1=4=1
\begin{equation}
\lim _{x \rightarrow 0} \frac{\int_{0}^{x}(x-t) \sin t^{2} \mathrm{~d} t}{\left(x^{2}+x^{3}\right)\left(1-\sqrt{1-x^{2}}\right)}
\end{equation}
bg
提示:看见积分,必定洛必达,但也要注意顺序。
x→0lim(x2+x3)(1−1−x2)∫0x(x−t)sint2 dt=x→0lim(x2+x3)⋅21x2x∫0xsint2 dt−∫0xtsint2 dt=x→0lim21x4x∫0xsint2 dt−∫0xtsint2 dt快使用洛必达,哼哼哈嘿!=x→0lim2x3∫0xsint2 dt+xsinx2−xsinx2=x→0lim6x2sinx2=61
\begin{equation}
\lim _{x \rightarrow 0}\left[\frac{1}{e^{x}-1}-\frac{1}{\ln (1+x)}\right]
\end{equation}
bg
提示:等价无穷小+洛必达法则
x→0lim[ex−11−ln(1+x)1]=x→0lim(ex−1)ln(1+x)ln(1+x)−ex+1=x→0limx⋅xln(1+x)−ex+1=x→0lim2x1+x1−ex上下都趋近于0,使用洛必达法则=21x→0limx1−ex(1+x)⋅x→0lim1+x1=21x→0limx′(1−ex(1+x))′=−21x→0lim(ex(2+x))=−1.
\begin{equation}
\lim _{x \rightarrow 0} \frac{x^{2} \sin \frac{1}{x}}{x+\sin x}
\end{equation}
bg
提示:请不要用洛必达!!
简单分析一下,可以发现这是一个00型极限,要是你手痒痒直接用了,就会陷入绝境: 原式 =limx→01+cosx2xsinx1−cosx1
实际上这道题的意义就是告诉你要注意洛必达的条件:求导后的极限存在才能用洛必达。
正解:原式 =x→0lim1+xsinxxsinx1=20=0
拉格朗日中值定理专区
如果函数 f(x) 在闭区间 [a,b] 上连续,在开区间 (a,b) 上可㝵,那么在开区间 (a,b) 内至少存在一点 ξ 使得 :
f′(ξ)=b−af(b)−f(a)
这个方法神奇的紧!
\begin{equation}
\lim _{x \rightarrow 0} \frac{\cos (\sin x)-\cos x}{\arcsin ^{4} x}
\end{equation}
bg
提示:
x→0limarcsin4xcos(sinx)−cosx=x→0limx4−sinξ⋅(sinx−x)
ξ介于sinx 与x之间,由夹逼定理可以得到limx→0xsinξ=1
x→0limarcsin4xcos(sinx)−cosx=x→0limx3−(sinx−x)=x→0lim3x21−cosx=61
驾轻就熟
\begin{equation}
\lim _{x \rightarrow 0}\left[\frac{a}{x}-\left(\frac{1}{x^{2}}-a^{2}\right) \ln (1+a x)\right](a \neq 0)
\end{equation}
bg
提示:等价无穷小推论
x→0lim[xa−(x21−a2)ln(1+ax)]=x→0lim[xa−x2ln(1+ax)]+x→0lima2ln(1+ax)=x→0limx2ax−ln(1+ax)=x→0limx221(ax)2(🥕−ln(1+🥕)∼21🥕2)=2a2.
\begin{equation}
\lim _{x \rightarrow+\infty} \frac{\sqrt{\left[(n x)^{n}+1\right]^{n+1}}}{(x+1)\left(x^{2}+2\right) \cdots\left(x^{n}+n\right)}
\end{equation}
bg
提示:找到相同的项,消消消,提取出来x,凑出来可以计算的无穷小。
x→+∞lim(x+1)(x2+2)⋯(xn+n)[(nx)n+1]n+1=x→+∞lim(1+x1)(1+x22)⋯(1+xnn)(nn+xn1)2n+1=n2n(n+1)
\begin{equation}
\lim_{x\to 0} \frac{x^2(e^x-1)}{\sqrt{1+\tan x}-\sqrt{1+ x}}
\end{equation}
bg
提示:泰勒展开式
tanx=n=1∑∞(2n)!B2n(−4)n(1−4n)x2n−1=x+31x3+152x5+31517x7+283562x9+1559251382x11+608107521844x13+638512875929569x15+⋯x∈(−1,1)
x→0lim1+tanx−1+xx2(ex−1)=x→0limtanx−xx3×(1+tanx+1+x)=x→0limtanx−xx3×2=x→0lim31x3x3×2=6
\begin{equation}
\lim_{x\to 0} \frac{\sqrt{4x^2+x-1}+x+1}{\sqrt{x^2+\sin x}}
\end{equation}
bg
提示:除以出现次数最多的,最讨厌的那一项。
x→0limx2+sinx4x2+x−1+x+1=x→∞lim1+x2sinx4+x1−x21+1+x1=14+1=3
\begin{equation}
\lim _{x \rightarrow 0} \frac{\int_{0}^{x} t \ln (1+t \sin t) \mathrm{d} t}{1-\cos x^{2}}
\end{equation}
bg
提示:判断极限类型+等价无穷小+洛必达法则
x→0lim1−cosx2∫0xtln(1+tsint)dt=x→0lim2x4∫0xtln(1+tsint)=x→0lim2x3xln(1+xsinx)=x→0lim2x3x(xsinx)=21
\begin{equation}
\lim _{x \rightarrow+\infty} \frac{\int_{1}^{x}\left(t^{2}\left(\mathrm{e}^{\frac{1}{t}}-1\right)-t\right) \mathrm{d} t}{x^{2} \ln \left(1+\frac{1}{x}\right)}
\end{equation}
bg
提示:判断极限类型+等价无穷小+洛必达法则
x→+∞limx2ln(1+x1)∫1x(t2(et1−1)−t)dt=x→+∞limx2⋅x1∫1x(t2(et1−1)−t)dt=x→+∞lim(x)′(∫1x(t2(et1−1)−t)dt)′=x→+∞lim(x2(ex1−1)−x)令 t=x1=x1t→0+limt2et−1−t上下都趋近于0,使用洛必达法则=t→0+lim2tet−1=21
\begin{equation}
\lim _{n \rightarrow \infty} \frac{n^{\frac{n^{2}+n+1}{n}}}{(n+1)^{n}}(\sqrt[n]{5}-1)
\end{equation}
bg
提示:对数字敏感+对公式敏感+剥洋葱法
🥕a🥕−1∼lna
====n→∞lim(n+1)nnnn2+n+1(n5−1)n→∞lim(n+1)nnn+1⋅nn(n5−1)n→∞lim(n+1)nnn1/n5−1n→∞lim(1+n1)n1⋅ln5eln5
\begin{equation}
\lim_{x\to 0}\frac{1}{\ln(1+x^2)}-\frac{1}{\sin^2x}
\end{equation}
bg
提示:对平方差敏感!
=x→0limsin2xln(1+x2)sin2x−ln(1+x2)=x→0limx4sin2x−ln(1+x2)=x→0limx4(sin2x−x2)−[ln(1+x2)−x2]=x→0limx4(sinx+x)(sinx−x)−x→0limx4−21x4=x→0limx4(2x)(−61x3)+21=−31+21=61
泰勒级数求极限专用区
\begin{equation}
\lim _{x \rightarrow 0} \frac{1+\frac{x^{2}}{2}-\sqrt{1+x^{2}}}{\left(\cos x-e^{x^{2}}\right) \sin x^{2}}
\end{equation}
bg
提示:基本泰勒展开式
1+x2ex2=(1+x2)21=1+21x2+2!21(21−1)x4+o(x4)=1+21x2−81x4+o(x4)cosx=1−2!x2+o(x2)=1−2x2+o(x2)=1+x2+o(x2)
x→0lim(cosx−ex2)sinx21+2x2−1+x2=x→0lim[(1−2x2+o(x2))−(1+x2+o(x2))]x21+2x2−(1+21x2−81x4+o(x4))=x→0lim−23x4+o(x4)81x4+o(x4)=−121
\begin{equation}
\lim _{n \rightarrow \infty}\left[\left(n^{3}-n^{2}+\frac{n}{2}\right) \mathrm{e}^{\frac{1}{n}}-\sqrt{1+n^{6}}\right]
\end{equation}
bg
提示:无。😠这谁想得到啊!!!
n→∞lim[(n3−n2+2n)en1−1+n6]=n→∞limn3[(1−n1+2n21)e∗1−1+n61]=n→∞limn3[(1−n1+2n21)−e−n11+n61]=n→∞limn3[(1−n1+2n21)−(1−n1+2n21−3!1n31+o(n31))(1+o(n31))]=61
蓦然回首
\begin{equation}
\lim _{x \rightarrow 0} \frac{\left(2+\sin x^{2}\right)^{x}-2^{\sin x}}{x^{3}}
\end{equation}
bg
提示:努力拼凑出来等价无穷小,提取相同的项,
\begin{aligned}&\lim _{x \rightarrow 0} \frac{\left(2+\sin x^{2}\right)^{x}-2^{\sin x}}{x^{3}}\\&=\lim _{x \rightarrow 0} \frac{\left(2+\sin x^{2}\right)^{x}-2^{x}}{x^{3}}+\lim _{x \rightarrow 0} \frac{2^{x}-2^{\sin x}}{x^{3}} \\&=\lim _{x \rightarrow 0} \frac{2^{x}\left[\left(1+\frac{\sin x^{2}}{2}\right)^{x}-1\right]}{x^{3}}+\lim _{x \rightarrow 0} \frac{2^{\sin x}\left(2^{x-\sin x}-1\right)}{x^{3}} \\&=\lim _{x \rightarrow 0} \frac{\frac{\sin x^{2}}{2} \cdot x}{x^{3}}+\lim _{x \rightarrow 0} \frac{(x-\sin x) \ln 2}{x^{3}} \\&=\lim _{x \rightarrow 0} \frac{\frac{1}{2} x^{3}}{x^{3}}+\lim _{x \rightarrow 0} \frac{\left(\frac{1}{6} x^{3}\right) \ln 2}{x^{3}} \\&=\frac{1}{2}+\frac{\ln 2}{6}\\\&=\frac{1}{2}+\ln \sqrt[6]{2} \end{aligned}
\begin{equation}
\lim _{x \rightarrow 1} \frac{x-x^{x}}{1-x+\ln x}
\end{equation}
bg
提示:努力拼凑出来等价无穷小,提取相同的项,
用换元法把趋向于1的x转换成趋向于0的h,多次拼凑并利用等价无穷小。
x→1lim1−x+lnxx−xx=h→0limln(1+h)−h(1+h)[1−(1+h)h]=h→0limh−ln(1+h)ehln(1+h)−1=h→0limh−ln(1+h)hln(1+h)=h→0limh−ln(1+h)h2=h→0lim1−1+h12h=2h→0lim(1+h)=2
往死里凑等价无穷小!!!
x→1lim1−x+lnxx−xx=x→1limln[1+(x−1)]−(x−1)]−x[e(x−1)lnx−1]=x→1lim−21(x−1)2−(x−1)lnx=2x→1lim(x−1)2(x−1)ln[1+(x−1)]=2x→1lim(x−1)2(x−1)2=2
\begin{equation}
\lim _{x \rightarrow+\infty}\left[\sqrt[3]{x^{3}+x^{2}+x+1}-\sqrt{x^{2}+x+1} \frac{\ln \left(\mathrm{e}^{x}+x\right)}{x}\right]
\end{equation}
bg
提示:要先推演一番,才能做出来😂
x→+∞limxln(ex+x)=x→+∞limxln[ex(1+exx)]=1+x→+∞limxln(1+exx)
======x→+∞lim[3x3+x2+x+1−x2+x+1xln(ex+x)]x→+∞lim(3x3+x2+x+1−x2+x+1)−limx→+∞x2+x+1ln(1+exx)x→+∞limx(31+x1+x21+x31−1+x1+x21)−0x→+∞limx(31+x1+x21+x31−1)−x→+∞limx(1+x1+x21−1)x→+∞limx[31(x1+x21+x31)]−x→+∞limx[21(x1+x21)]31−21−61
\begin{equation}
\lim _{x \rightarrow 0} \frac{\int_{0}^{x^{2}} f(t) \mathrm{d} t}{x^{2} \int_{0}^{x} f(t) \mathrm{d} t}\quad f(0)=0,f'(0)\ne 0
\end{equation}
bg
提示:使用了两次洛必达法则(标蓝部分),以及导数的定义(精妙之处)
x→0limx2∫0xf(t)dt∫0x2f(t)dt=x→0lim2x∫0xf(t)dt+x2f(x)2xf(x2)=x→0lim2∫0xf(t)dt+xf(x)2f(x2)=x→0lim3f(x)+xf′(x)4xf′(x2)=x→0limx3f(x)+f′(x)4f′(x2)=3f′(0)+f′(0)4f′(0)=1
\begin{equation}
\text { 设函数 } f(x) \text { 可导, 求极限 } \lim _{x \rightarrow x_{0}} \frac{x_{0} f(x)-x f\left(x_{0}\right)}{x-x_{0}}
\end{equation}
bg
提示:使用导数的定义,尽力去凑导数定义式的形式,另外,值得注意的是:可导不代表着该函数在任意点处的极限都存在
x→x0limx−x0x0f(x)−xf(x0)=x→x0limx−x0x0f(x)−x0f(x0)−x→x0limx−x0xf(x0)−x0f(x0)=x0x→x0limx−x0f(x)−f(x0)−f(x0)=x0f′(x0)−f(x0)
经验总结
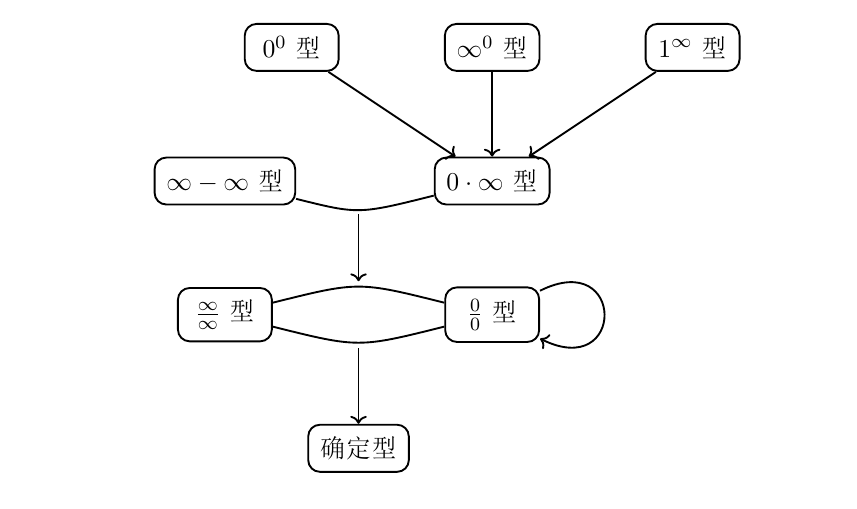
对于求极限问题,首先要判断所求极限的类型,若属于确定型,就按确定型中具体类型进行计算;若属于待定型,则看属于待定型中的“商型”、“积差型”还是“幂指型”,其中“商型”是最基础的待定型,“积差型”和“幂指型”都要经过转化最终转化为“商型”进行计算,其中,1∞ 型除了可以转化为“商型”进行计算外,还可以利用第二重要极限的推广进行计算。确定所求极限的类型至关重要,只有知道所求极限的类型了,才可以按照相应类型的方法进行计算。
等价无穷小要义
当🥕→0时
🥕相当于一个函数,最常见的的就是x了
🥕∼sin(🥕)∼tan(🥕)∼e🥕−1∼ln(1+🥕)∼arcsin(🥕)∼arctan(🥕)
1−cos(🥕)∼21🥕2🥕−sin(🥕)∼61🥕3
1−cos(🥕)∼21🥕2⟹1−ncos(🥕)∼2nx2−n+1
ln(🥕+1+🥕2)∼🥕
ln(1+🥕)∼🥕⟹log🥬(1+🥕)∼ln🥬🥕
e🥕−1∼🥕⟹🥬🥕−1∼🥕ln🥬
(1+🥕)🥬−1∼🥬🥕🥕🥬🥕−1∼ln🥬
加减法使用等价无穷小
口诀: 加不反,减不同,等价随便换
若 α∼α′,β∼β′, 且 limβα=A=−1, 则 α+β∼α′+β′;
若 α∼α′, β∼β′, 且 limβα=A=1, 则 α−β∼α′−β′.
*等价无穷小的推导
此部分从属于紫晶计划·铁石 笔尖学术
泰勒展开式
泰勒级数(英语:Taylor series)用无限项连加式——级数来表示一个函数,这些相加的项由函数在某一点的导数求得。泰勒级数是以于1715年发表了泰勒公式的英国数学家布鲁克·泰勒(Sir Brook Taylor)来命名的。通过函数在自变量零点的导数求得的泰勒级数又叫做麦克劳林级数(英语:Maclaurin series),以苏格兰数学家科林·麦克劳林的名字命名。所以,我们经常用的所谓的“泰勒展开式”实际上应该称为“麦克劳林级数”。
刚才差点又陷入误区,准备把无穷级数全部复习一遍,之后再来写这篇文章。实际上,很多东西,只有很少一部分是关键所在,理解了关键,就没有必要从头再来。况且,兴致是会消减的,学着学着就把写文章的激情磨光了,这可能也是多巴胺的规律之一吧。所以本文就从关键开始,从核心开始,以紫晶计划的要义“取其精华,弃其糟粕。”为指导,把我想表达的表达出来。
本文的主要依据是泰勒级数,泰勒级数的标准形式为:
n=0∑∞n!f(n)(a)(x−a)n=f(a)+1!f′(a)(x−a)+2!f′′(a)(x−a)2+3!f′′′(a)(x−a)3+⋯
以下为常见的麦克劳林展开式(不要怕,只需要记住五个我标注为紫色的,就足以推导出大多数等价无穷小):
bg
1−x1=n=0∑∞xn=1+x+x2+⋯+xn+⋯∀x:∣x∣<1(1+x)α=n=0∑∞(nα)xn=1+αx+2!α(α−1)x2+⋯+n!α(α−1)⋯(α−n+1)xn+⋯∀x:∣x∣<1,∀α∈Cex=n=0∑∞n!xn=1+x+2!x2+3!x3+⋯+n!xn+⋯∀xax=exlna=n=0∑∞n!(xlna)n=1+xlna+2!(xlna)2+3!(xlna)3+⋯+n!(xlna)n+⋯∀xln(1−x)=−n=1∑∞nxn=−x−2x2−3x3−⋯−nxn−⋯∀x∈[−1,1)ln(1+x)=n=1∑∞n(−1)n+1xn=x−2x2+3x3−⋯+n(−1)n+1xn+⋯∀x∈(−1,1]loga(1+x)=lnaln(1+x)=lna1n=1∑∞n(−1)n+1xn=lnax−2lnax2+3lnax3−⋯+nlna(−1)n+1xn+⋯∀x∈(−1,1]
sinxcosxtanxsecxarcsinxarccosxarctanx=n=0∑∞(2n+1)!(−1)nx2n+1=n=0∑∞(2n)!(−1)nx2n=n=1∑∞(2n)!B2n(−4)n(1−4n)x2n−1=n=0∑∞(2n)!(−1)nE2nx2n=n=0∑∞4n(n!)2(2n+1)(2n)!x2n+1=2π−arcsinx=2π−n=0∑∞4n(n!)2(2n+1)(2n)!x2n+1=n=0∑∞2n+1(−1)nx2n+1=x−3!x3+5!x5−⋯=1−2!x2+4!x4−⋯=x+3x3+152x5+⋯=1+2x2+245x4+⋯=x+6x3+403x5+⋯=2π−x−6x3−403x5+⋯=x−3x3+5x5−⋯∀x∀x∀x:∣x∣<2π∀x:∣x∣<2π∀x:∣x∣≤1∀x:∣x∣≤1∀x:∣x∣≤1, x=±i
等价运算符
此部分为本人杜撰,结论不够准确严谨,但应付等价无穷小的推导应该绰绰有余。如有错误,还望指正🐰。
等价无穷小的不严格定义:
当x→0时,两个函数A(x),B(x)同时收敛于一个常数(英文:constant) C,那么这两个函数为x→0时等价无穷小,记作A(x)∼B(x)
下面介绍一下等价无穷小运算符"∼"的运算规律,当x→0时,有如下运算规律:
-
if A(x)∼B(x),B(x)∼C(x)then A(x)∼C(x)
-
if\ A(x)\sim B(x),C\ is\ a\ constant,\ then \
A(x)⋅C∼B(x)⋅C
A(x)±C∼B(x)±C
-
if A(x)∼a ,B(x)∼b
A(x)⋅B(x)∼a⋅b
B(x)A(x)∼ba
A(x)+B(x)∼a+bif and only if x→0limB(x)A(x)=−1
A(x)−B(x)∼a−bif and only if x→0limB(x)A(x)=1
值得注意的是,对于A(x)−B(x)这种情形,往往会出现x→0limB(x)A(x)=1, 这个时候可以利用下文所讲的泰勒展开式来进行等价😎
-
当函数A(x)在x→0处,收敛于某一值,且其可以展开为如下的多项式a0+a1x+a2x2+⋯anxn,则:A(x)∼a0+a1x+a2x2+⋯anxn
推论1:这个和高阶等价无穷小有关,应该有更严谨的表达,但鄙人懒得翻了,就按我的意思表达吧。
When A(x)=a0+a1x+a2x2+⋯anxn, B(x)=b0+b1x+b2x2+⋯+bnxn thenx→0limB(x)A(x)==b0+b1x+b2x2+⋯+bnxna0+a1x+a2x2+⋯anxn if n<m
推论2:泰勒展开式移项A(x)−a0−a1x−⋯ajxj∼aj+1xj+1+⋯anxn
等价无穷小·推导Plus+Pro
泰勒展开式等价无穷小
由于较高阶次的项,考试也不会考,写下来也麻烦的紧,这里就利用最高次幂为二或三的展开式来推导常见的无穷小。
sinxarcsinxtanxarctanxcosxexaxln(1+x)loga(1+x)(1+x)a1+x11−x1∼x∼x∼x∼x∼1∼1∼1∼x∼lnax∼1∼1∼1∼x−6x3∼x+6x3∼x+3x3∼x−3x3∼1−2x2∼1+x∼1+xlna∼x−2x2∼lnax−2lnax2∼1+ax∼1−x∼1+x∼1+x+2x2∼1+xlna+2(xlna)2∼1+ax+2a(a−1)x2∼1−x+x2∼1+x+x2
这些是原始的等价无穷小,亦可以看作出题者的后台
根据等价运算符的运算规律,特别是推论2,我们可以很容易得到以下推论:
x∼sin(x)∼tan(x)∼ex−1∼ln(1+x)∼arcsin(x)∼arctan(x)
sinx−xarcsinx−xtanx−xarctanx−xcosx−1ex−1ax−1ln(1+x)−xloga(1+x)−lnax(1+x)a−11+x−x1−xx∼−6x3∼6x3∼3x3∼−3x3∼−2x2∼x∼xlna∼−2x2∼−2lnax2∼ax∼−x∼x∼x+2x2∼xlna+2(xlna)2∼ax+2a(a−1)x2∼−x+x2∼x+x2
等价无穷小·推导 50
通过核心公式(泰勒展开式中标紫的地方):sinx,tanx,ex,ln(x+1),加上简单的加减乘除,三角函数运算,对数运算,以及上文的等价运算,可以很方便的推导出其他的等价无穷小,太累了,过程省略,给你张图,慢慢推导吧