✍文章痕迹
抄写 撰写了定理的基本定义参考《微积分解题方法与技巧》[^1]添加了几个例子 [x] 定义与方法 [ ] 题型与应用方法 [ ] 真题练习 [ ] 自押题
微分中值定理是罗尔定理、拉格郎日中值定理 和柯西中值定理的统称。其中:
拉格朗日中值定理是 微分中值定理的核心,它给出了导数值与函数值之间的某种定理关系,可以应用它来证明一些等式或不等式 。
罗尔定理可看成特殊情况下的拉格朗日中值定理,它可以证明等式,还有重要应用是可以解决某些方程根的存在性问题 。
柯西中值定理是拉格朗日中值定理的推广,它可以用来证明等式或不等式 。应用导数的局部性质研究函数全局性质 的重要工具。它使得导数理论用于函数形态的研究成为可能,显示了导数理论、微分学的强大功能和广泛的应用性。
——陈阳、王涛「浅谈微分中值定理证明及应用题目」
各种小定理
最值定理f ( x ) f(x) f ( x ) [ a , b ] [a,b] [ a , b ] m ≤ f ( x ) ≤ M m\le f(x)\le M m ≤ f ( x ) ≤ M
(其中m , M m,M m , M
若函数f ( x ) f(x) f ( x ) [ a , b ] [a,b] [ a , b ] m , M m,M m , M m ≤ C ≤ M m\le C \le M m ≤ C ≤ M
∃ ξ ∈ [ a , b ] , f ( ξ ) = C \exists\xi\in[a,b],f(\xi)=C ∃ ξ ∈ [ a , b ] , f ( ξ ) = C
平均值原理a < x 1 < x 2 < ⋯ < x n < b a<x_1<x_2<\cdots<x_n<b a < x 1 < x 2 < ⋯ < x n < b [ x 1 , x n ] \left[x_1, x_n\right] [ x 1 , x n ] ξ \xi ξ f ( ξ ) = f ( x 1 ) + f ( x 2 ) + ⋯ + f ( x n ) n \displaystyle f(\xi)=\frac{f\left(x_1\right)+f\left(x_2\right)+\cdots+f\left(x_n\right)}{n} f ( ξ ) = n f ( x 1 ) + f ( x 2 ) + ⋯ + f ( x n )
零点定理f ( x ) f(x) f ( x ) [ a , b ] [a,b] [ a , b ] f ( a ) ⋅ f ( b ) < 0 f(a) \cdot f(b)<0 f ( a ) ⋅ f ( b ) < 0 ξ ∈ ( a , b ) \xi \in(a, b) ξ ∈ ( a , b ) f ( ξ ) = 0 f(\xi)=0 f ( ξ ) = 0 费马定理f ( X ) f(X) f ( X ) x 0 x_0 x 0 f ′ ( x 0 ) = 0 f^{'}(x_0)=0 f ′ ( x 0 ) = 0
若函数f ( x ) f(x) f ( x )
在闭区间 [ a , b ] [a,b] [ a , b ]
在开区间( a , b ) (a,b) ( a , b )
端点值相等f ( a ) = f ( b ) f(a)=f(b) f ( a ) = f ( b )
则至少存在一点ξ ∈ ( a , b ) \xi\in(a,b) ξ ∈ ( a , b ) f ′ ( ξ ) = 0 \color{blue}f^{'}(\xi)=0 f ′ ( ξ ) = 0
推广:把端点取值范围进行推广,可以得到更为宽泛的罗尔定理。
lim x → a + f ( x ) = lim x → b − f ( x ) = A \displaystyle \lim_{x\to a^+}f(x) =\lim_{x\to b^-}f(x) = A x → a + lim f ( x ) = x → b − lim f ( x ) = A A A A ± ∞ ⟹ ∃ ξ ∈ ( a , b ) , f ′ ( ξ ) = 0 \pm\infty\Longrightarrow \exists \xi\in(a,b) , f^{'}(\xi)=0 ± ∞ ⟹ ∃ ξ ∈ ( a , b ) , f ′ ( ξ ) = 0
lim x → − ∞ f ( x ) = lim x → + ∞ f ( x ) = A ⟹ ∃ ξ ∈ ( − ∞ , + ∞ ) , f ′ ( ξ ) = 0 \displaystyle \lim_{x\to -\infty}f(x) =\lim_{x\to +\infty}f(x) = A \Longrightarrow \exists\xi\in(-\infty,+\infty),f^{'}(\xi)=0 x → − ∞ lim f ( x ) = x → + ∞ lim f ( x ) = A ⟹ ∃ ξ ∈ ( − ∞ , + ∞ ) , f ′ ( ξ ) = 0
利用f ′ ( ξ ) = 0 f^{\prime}(\xi)=0 f ′ ( ξ ) = 0
设函数 f ( x ) , g ( x ) f(x), g(x) f ( x ) , g ( x ) [ a , b ] [a, b] [ a , b ] ( a , b ) (a, b) ( a , b ) f ( a ) = g ( a ) , f ( b ) = g ( b ) f(a)=g(a), f(b)=g(b) f ( a ) = g ( a ) , f ( b ) = g ( b ) ξ ∈ ( a , b ) \xi \in(a, b) ξ ∈ ( a , b ) f ′ ′ ( ξ ) = f^{\prime \prime}(\xi)= f ′ ′ ( ξ ) = g ′ ′ ( ξ ) g^{\prime \prime}(\xi) g ′ ′ ( ξ )
来自参考文献一·P126·例二
思路很常规,用了罗尔定理,但题设中最大值点不明确,需要分类讨论 。第二步需要借用零点存在定理证明另一个点为零。
证明: 令 F ( x ) = f ( x ) − g ( x ) F(x)=f(x)-g(x) F ( x ) = f ( x ) − g ( x ) F ( x ) F(x) F ( x ) [ a , b ] [a, b] [ a , b ] ( a , b ) (a, b) ( a , b )
F ( a ) = F ( b ) = 0. F(a)=F(b)=0 . F ( a ) = F ( b ) = 0 .
当函数 f ( x ) , g ( x ) f(x), g(x) f ( x ) , g ( x ) ( a , b ) (a, b) ( a , b ) 同一点 c c c F ( c ) = 0 F(c)=0 F ( c ) = 0 F ( x ) F(x) F ( x ) [ a , c ] , [ c , b ] [a, c],[c, b] [ a , c ] , [ c , b ] ξ 1 ∈ ( a , c ) , ξ 2 ∈ ( c , b ) \xi_1 \in(a, c), \xi_2 \in(c, b) ξ 1 ∈ ( a , c ) , ξ 2 ∈ ( c , b ) F ′ ( ξ 1 ) = F ′ ( ξ 2 ) = 0 , F^{\prime}\left(\xi_1\right)=F^{\prime}\left(\xi_2\right)=0, F ′ ( ξ 1 ) = F ′ ( ξ 2 ) = 0 ,
进一步, 对函数 F ′ ( x ) F^{\prime}(x) F ′ ( x ) [ ξ 1 , ξ 2 ] \left[\xi_1, \xi_2\right] [ ξ 1 , ξ 2 ] ξ ∈ ( ξ 1 , ξ 2 ) \xi \in\left(\xi_1, \xi_2\right) ξ ∈ ( ξ 1 , ξ 2 ) F ′ ′ F^{\prime \prime} F ′ ′ ( ξ ) = 0 (\xi)=0 ( ξ ) = 0 f ′ ′ ( ξ ) = g ′ ′ ( ξ ) f^{\prime \prime}(\xi)=g^{\prime \prime}(\xi) f ′ ′ ( ξ ) = g ′ ′ ( ξ )
当函数 f ( x ) , g ( x ) f(x), g(x) f ( x ) , g ( x ) ( a , b ) (a, b) ( a , b ) 不同 点 c , d ( c < d ) c, d(c<d) c , d ( c < d ) f ( c ) = g f(c)=g f ( c ) = g ( d ) = M (d)=M ( d ) = M M M M F ( c ) = f ( c ) − g ( c ) > 0 , F ( d ) = f ( d ) − g ( d ) < 0 , F(c)=f(c)-g(c)>0, \quad F(d)=f(d)-g(d)<0, F ( c ) = f ( c ) − g ( c ) > 0 , F ( d ) = f ( d ) − g ( d ) < 0 ,
由零点定理知, 存在 η ∈ ( c , d ) \eta \in(c, d) η ∈ ( c , d ) F ( η ) = 0 F(\eta)=0 F ( η ) = 0 F ( x ) F(x) F ( x ) [ a , η ] [a, \eta] [ a , η ] [ η , b ] [\eta, b] [ η , b ] ξ 1 ∈ ( a , η ) , ξ 2 ∈ ( η , b ) \xi_1 \in(a, \eta), \xi_2 \in(\eta, b) ξ 1 ∈ ( a , η ) , ξ 2 ∈ ( η , b )
F ′ ( ξ 1 ) = F ′ ( ξ 2 ) = 0 , F^{\prime}\left(\xi_1\right)=F^{\prime}\left(\xi_2\right)=0, F ′ ( ξ 1 ) = F ′ ( ξ 2 ) = 0 ,
进一步, 对函数 F ′ ( x ) F^{\prime}(x) F ′ ( x ) [ ξ 1 , ξ 2 ] \left[\xi_1, \xi_2\right] [ ξ 1 , ξ 2 ] ξ ∈ ( ξ 1 , ξ 2 ) \xi \in\left(\xi_1, \xi_2\right) ξ ∈ ( ξ 1 , ξ 2 ) F ′ ′ ( ξ ) = 0 F^{\prime \prime}(\xi)=0 F ′ ′ ( ξ ) = 0 F ′ ′ ( ξ ) = g ′ ′ ( ξ ) F^{\prime \prime}(\xi)=g^{\prime \prime}(\xi) F ′ ′ ( ξ ) = g ′ ′ ( ξ )
当题目中要求证明“至少存在一点ξ ∈ ( a , b ) \xi\in(a,b) ξ ∈ ( a , b ) f ( n ) ( x ) f^{(n)}(x) f ( n ) ( x ) f ( m ) ( x ) f^{(m)}(x) f ( m ) ( x )
变形 → 代换 → 还原 → 合并 \text{变形}\to\text{代换}\to\text{还原}\to\text{合并}
变形 → 代换 → 还原 → 合并
而对于没有特征或一般的情形我们可以直接把题设上移项直接转化成F ( x ) F(x) F ( x )
形式
辅助函数
f ( x ) f ′ ( x ) f(x) f^{\prime}(x) f ( x ) f ′ ( x ) F ( x ) = f 2 ( x ) F(x)=f^2(x) F ( x ) = f 2 ( x )
f ′ ( x ) f ( x ) \frac{f^{\prime}(x)}{f(x)} f ( x ) f ′ ( x ) F ( x ) = ln f ( x ) F(x)=\ln f(x) F ( x ) = ln f ( x )
[ f ′ ( x ) ] 2 + f ( x ) f ′ ′ ( x ) \left[f^{\prime}(x)\right]^2+f(x) f^{\prime \prime}(x) [ f ′ ( x ) ] 2 + f ( x ) f ′ ′ ( x ) F ( x ) = f ( x ) f ′ ( x ) F(x)=f(x) f^{\prime}(x) F ( x ) = f ( x ) f ′ ( x )
f ′ ( x ) + f ( x ) φ ′ ( x ) f^{\prime}(x)+f(x) \varphi^{\prime}(x) f ′ ( x ) + f ( x ) φ ′ ( x ) F ( x ) = f ( x ) e φ ( x ) F(x)=f(x) \mathrm{e}^{\varphi(x)} F ( x ) = f ( x ) e φ ( x )
f ′ ( x ) x − f ( x ) , x ≠ 0 f^{\prime}(x) x-f(x), x \neq 0 f ′ ( x ) x − f ( x ) , x = 0 F ( x ) = f ( x ) x \displaystyle F(x)=\frac{f(x)}{x} F ( x ) = x f ( x )
f ′ ′ ( x ) f ( x ) − [ f ′ ( x ) ] 2 , f ( x ) ≠ 0 f^{\prime \prime}(x) f(x)-\left[f^{\prime}(x)\right]^2, f(x) \neq 0 f ′ ′ ( x ) f ( x ) − [ f ′ ( x ) ] 2 , f ( x ) = 0 F ( x ) = f ′ ( x ) f ( x ) \displaystyle F(x)=\frac{f^{\prime}(x)}{f(x)} F ( x ) = f ( x ) f ′ ( x )
更复杂一点的辅助函数有:
形式
辅助函数
f ′ ( ξ ) + λ f ( ξ ) = 0 f^{\prime}(\xi)+\lambda f(\xi)=0 f ′ ( ξ ) + λ f ( ξ ) = 0 λ \lambda λ F ( x ) = f ( x ) e λ x F(x)=f(x) \mathrm{e}^{\lambda x} F ( x ) = f ( x ) e λ x
f ′ ( ξ ) + 2 λ ξ f ( ξ ) = 0 f^{\prime}(\xi)+2 \lambda \xi f(\xi)=0 f ′ ( ξ ) + 2 λ ξ f ( ξ ) = 0 λ \lambda λ F ( x ) = f ( x ) e λ x 2 F(x)=f(x) \mathrm{e}^{\lambda x^2} F ( x ) = f ( x ) e λ x 2
ξ f ′ ( ξ ) − n f ( ξ ) = 0 \xi f^{\prime}(\xi)-n f(\xi)=0 ξ f ′ ( ξ ) − n f ( ξ ) = 0 n n n F ( x ) = f ( x ) x n F(x)=\frac{f(x)}{x^n} F ( x ) = x n f ( x )
f ′ ( ξ ) + g ( ξ ) f ( ξ ) = 0 f^{\prime}(\xi)+g(\xi) f(\xi)=0 f ′ ( ξ ) + g ( ξ ) f ( ξ ) = 0 F ( x ) = f ( x ) e ∫ g ( x ) d x F(x)=f(x) \mathrm{e}^{\int g(x) d x} F ( x ) = f ( x ) e ∫ g ( x ) d x
可以发现当出现ξ f ( ξ ) ′ \xi f(\xi)^\prime ξ f ( ξ ) ′ ξ f ( ξ ) \xi f(\xi) ξ f ( ξ )
这里举几个构造辅助函数的示例:
示例一:证明拉格朗日中值定理
以证明拉格朗日中值定理为例,要求证明的等式为
f ′ ( ξ ) = f ( b ) − f ( a ) b − a f^{\prime}(\xi)=\frac{f(b)-f(a)}{b-a} f ′ ( ξ ) = b − a f ( b ) − f ( a )
我们可以按照变形-代换-还原-合并 四步这样构建辅助函数:
1 : 变形 f ′ ( ξ ) − f ( b ) − f ( a ) b − a = 0 2 : 代换 f ′ ( x ) − f ( b ) − f ( a ) b − a = 0 3 : 还原 [ f ( x ) ] ′ − [ f ( b ) − f ( a ) b − a ⋅ x ] ′ = 0 4 : 合并 [ f ( x ) − f ( b ) − f ( a ) b − a ⋅ x ] ′ = 0 💥构造辅助函数 F ( x ) = f ( x ) − f ( b ) − f ( a ) b − a ⋅ x \begin{aligned}\textcolor{pink}{1:变形}\qquad&f^{\prime}(\xi)-\frac{f(b)-f(a)}{b-a}=0\\\textcolor{orange}{2:代换}\qquad&f^{\prime}(\textcolor{red}{x})-\frac{f(b)-f(a)}{b-a}=0\\\textcolor{green}{3:还原}\qquad&[f(x)]^{\prime}-[\frac{f(b)-f(a)}{b-a}\cdot x]^{\prime}=0\\\textcolor{teal}{4:合并}\qquad&[f(x)-\frac{f(b)-f(a)}{b-a}\cdot x]^{\prime}=0\\\textcolor{purple}{💥构造辅助函数}\qquad&F(x)=f(x)-\frac{f(b)-f(a)}{b-a}\cdot x\end{aligned} 1 : 变 形 2 : 代 换 3 : 还 原 4 : 合 并 💥 构 造 辅 助 函 数 f ′ ( ξ ) − b − a f ( b ) − f ( a ) = 0 f ′ ( x ) − b − a f ( b ) − f ( a ) = 0 [ f ( x ) ] ′ − [ b − a f ( b ) − f ( a ) ⋅ x ] ′ = 0 [ f ( x ) − b − a f ( b ) − f ( a ) ⋅ x ] ′ = 0 F ( x ) = f ( x ) − b − a f ( b ) − f ( a ) ⋅ x
然后发现F ( a ) = F ( b ) F(a)=F(b) F ( a ) = F ( b ) F ( x ) ′ = 0 F(x)^\prime=0 F ( x ) ′ = 0
示例二:比示例一稍微复杂的辅助函数
这是去年不知道在哪里找的题目,当时标记的是“好题”,现在看看居然跟拉格朗日中值定理那么像,所以我们依旧可以按照变形-代换-还原-合并 四步来构建辅助函数。这道题要求证明的等式为:
f ( ξ ) − ξ f ′ ( ξ ) = a f ( b ) − b f ( a ) a − b f(\xi)-\xi f^\prime(\xi)=\frac{af(b)-bf(a)}{a-b} f ( ξ ) − ξ f ′ ( ξ ) = a − b a f ( b ) − b f ( a )
1 : 变形 ξ f ′ ( ξ ) − f ( ξ ) + a f ( b ) − b f ( a ) a − b = 0 2 : 代换 x f ′ ( x ) − f ( x ) + a f ( b ) − b f ( a ) a − b = 0 3 : 还原 x f ′ ( x ) − f ( x ) + a f ( b ) − b f ( a ) a − b x 2 = 0 4 : 合并 [ f ( x ) − a f ( b ) − b f ( a ) a − b x ] ′ = 0 💥构造辅助函数 F ( x ) = f ( x ) − a f ( b ) − b f ( a ) a − b x \begin{aligned}\textcolor{pink}{1:变形}\qquad&\xi f^\prime(\xi)-f(\xi)+\frac{af(b)-bf(a)}{a-b}=0\\\textcolor{orange}{2:代换}\qquad&x f^\prime(x)-f(x)+\frac{af(b)-bf(a)}{a-b}=0\\\textcolor{green}{3:还原}\qquad&\frac{x f^\prime(x)-f(x)+\frac{af(b)-bf(a)}{a-b}}{x^2}=0\\\textcolor{teal}{4:合并}\qquad&[\frac{f(x)-\frac{af(b)-bf(a)}{a-b}}{x}]^\prime=0\\\textcolor{purple}{💥构造辅助函数}\qquad&F(x)=\frac{f(x)-\frac{af(b)-bf(a)}{a-b}}{x}\end{aligned} 1 : 变 形 2 : 代 换 3 : 还 原 4 : 合 并 💥 构 造 辅 助 函 数 ξ f ′ ( ξ ) − f ( ξ ) + a − b a f ( b ) − b f ( a ) = 0 x f ′ ( x ) − f ( x ) + a − b a f ( b ) − b f ( a ) = 0 x 2 x f ′ ( x ) − f ( x ) + a − b a f ( b ) − b f ( a ) = 0 [ x f ( x ) − a − b a f ( b ) − b f ( a ) ] ′ = 0 F ( x ) = x f ( x ) − a − b a f ( b ) − b f ( a )
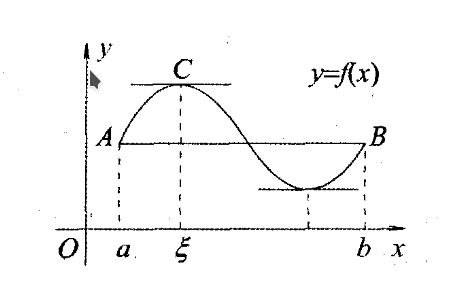
若函数f ( x ) f(x) f ( x )
在闭区间 [ a , b ] [a,b] [ a , b ]
在开区间( a , b ) (a,b) ( a , b )
则至少存在一点ξ ∈ ( a , b ) \xi\in(a,b) ξ ∈ ( a , b ) f ( a ) − f ( b ) = f ′ ( ξ ) ( b − a ) \color{blue}f(a)-f(b)=f^{'}(\xi)(b-a) f ( a ) − f ( b ) = f ′ ( ξ ) ( b − a )
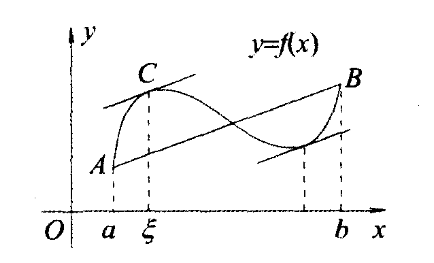
若函数f ( x ) f(x) f ( x )
在闭区间[ a , b ] [a,b] [ a , b ]
在开区间( a , b ) (a,b) ( a , b ) f ′ ( x ) ≠ 0 f^{'}(x)\ne 0 f ′ ( x ) = 0 ξ ∈ ( a , b ) \xi\in(a,b) ξ ∈ ( a , b ) F ( a ) − F ( b ) f ( b ) − f ( a ) = F ′ ( ξ ) f ′ ( ξ ) \color{blue} \displaystyle \frac{F(a)-F(b)}{f(b)-f(a)}=\frac{F^{'}(\xi)}{f^{'}(\xi)} f ( b ) − f ( a ) F ( a ) − F ( b ) = f ′ ( ξ ) F ′ ( ξ )
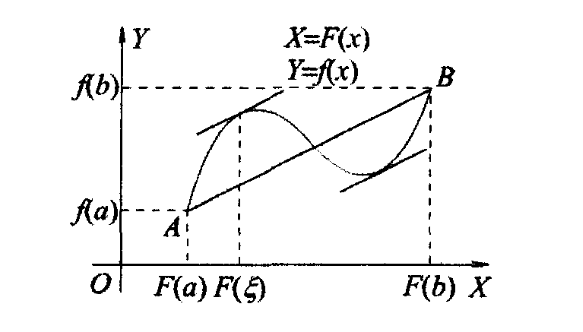
用参数方程来理解柯西中值定理的几何意义更容易:
若上图弧线A B AB A B { x = g ( t ) , y = f ( t ) , \left\{\begin{array}{l}
x=g(t), \\
y=f(t),
\end{array}\right. { x = g ( t ) , y = f ( t ) , a ≤ t ≤ b a\le t\le b a ≤ t ≤ b A A A t = a t=a t = a A A A t = b t=b t = b A B AB A B f ( b ) − f ( a ) g ( b ) − g ( a ) \frac{f(b)-f(a)}{g(b)-g(a)} g ( b ) − g ( a ) f ( b ) − f ( a ) C C C f ′ ( ξ ) g ′ ( ξ ) \frac{f^{\prime}(\xi)}{g^{\prime}(\xi)} g ′ ( ξ ) f ′ ( ξ ) C C C A B A B A B f ′ ( ξ ) g ′ ( ξ ) = f ( b ) − f ( a ) g ( b ) − g ( a ) \frac{f^{\prime}(\xi)}{g^{\prime}(\xi)}=\frac{f(b)-f(a)}{g(b)-g(a)} g ′ ( ξ ) f ′ ( ξ ) = g ( b ) − g ( a ) f ( b ) − f ( a )