本文为《传热学笔记》的分支，在后期精简过程中会被清理合并。

介质 传热机理
气体 分子不规则运动
导电固体 自由电子运动
不导电固体 （声子）晶格结构振动
液体 综合气体与固体

引入温度场：定义各个时刻物体中各点温度所组成的集合，物体的温度场时坐标与时间的函数：t=f(x,y,x,z,τ)t=f(x,y,x,z,\tau)，如果为稳态问题，则时间为定值，即t=f(x,y,x,z)t=f(x,y,x,z)

导热基本定律

在导热过程中，单位时间内通过给定截面积的导热率量，正比于垂直于该截面方向上的温度变化率和截面面积，热量传递的方向与温度升高的方向相反。

Φ=−λA∂t∂x\varPhi=-\lambda A \frac{\partial t}{\partial x}

q=−A∂t∂xq= - A \frac{\partial t}{\partial x}

当物体的温度式三个坐标的函数时，热流密度式是矢量，上式为沿着x方向的矢量，傅里叶导热定律的一般数学表达式为：

q=−λgrad t=−λ∂t∂xnq= - \lambda grad\ t= - \lambda \frac{\partial t}{\partial x }n

grad tgrad\ t为空间中某点的温度梯度，n{n} 为通过该点的等温线上的单位矢量。

导热系数

导热系数的数值取决于物质的种类和温度等因素。

导热系数小于0.08W/(m⋅K)W/(m\cdot K)的材料被称为保温材料，如矿渣棉、硅藻土、岩棉板、膨胀珍珠岩、SiO2SiO_2气凝胶等。

降低导热系数的方法：使用空心结构（如将标准黏土砖从实心改成空心率为40%40\%的空心砖，其当量传热系数可以减少大约50%50\%左右）

导热微分方程笔记

目标案例

现有一加热炉，炉壁由四层结构构成：最里层为厚65mm的耐火砖，第二层为65mm的隔热层（材质标注为聚轻球，不知道明确材质），第三层为70mm的保温棉，最外层为160mm的保温块（材质未知）。

在炉内温度为1100摄氏度时，炉壁平均为65摄氏度，计算每平方米每小时的散热量。

【分析】：本问题忽略炉顶炉底，仅分析炉壁散热，可以简化为传热学中一维稳态导热问题中的多层平壁模型[1]（忽略各层间的接触热阻，层与层之间不发生温度降低），此模型求解计算时需要知道：

  1. 各层的厚度：可在工程图中获得数据，
  2. 各层的导热系数：材料导热系数与温度有关，可假设一估计值，而后进行迭代求解。
  3. 最内最外层的温度：内层通过热电偶获得，外层通过测温仪测得。

收集数据简单整理如下图：

【导热系数计算】：工程上材料的导热系数一般都是温度的函数，这就意味着需要知道温度才能求得导热系数，然而层间温度本身是未知的，甚至有些材料（如最外层的保温块）本身也是未知的。在这种情况下可通过迭代法求解：估计一个大概的导热系数，用此导热系数来估计出层间温度，与已知的最内侧、最外侧温度进行比较，偏差超过允许值则重新估计，进行迭代，直到逼近到合理数值。

  1. 将温度分布看作线性——从炉内到炉外依次降低，来估计层间温度。即 Δt=t0−t4∑δ=1100−6565+65+70+160=2.875\Delta t = \frac{t_0-t_4}{\sum \delta}=\frac{1100-65}{65+65+70+160}=2.875℃/mm
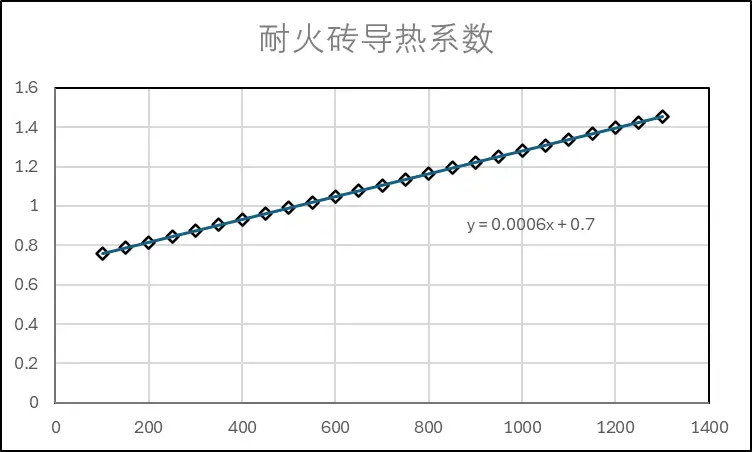
  2. 查询材料的导热系数经验计算公式，根据层间温度来估计导热系数：
材料层 厚度(mm) 材质 参考导热系数λ₀ (W/m·K) 温度系数b (K⁻¹) 估计层间温度
耐火砖 65 高铝耐火砖 1.30 0.0006 913.1°C
聚轻球 65 轻质氧化铝球 0.15 0.0003 726.2°C
保温棉 70 硅酸铝纤维棉 0.08 0.0001 525.0°C
保温块 160 微孔硅酸钙板 0.07 0.0002 –

查手册得到的耐火砖导热系数值

按照思路撰写迭代程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
import numpy as np

def calculate_lambda(T, lambda0, b):
    return lambda0 * (1 + b * T)

def solve_furnace_wall(T_inner, T_outer, layers, tol=0.5, max_iter=100):
    total_thickness = sum(layer[0] for layer in layers)
    T_interfaces = [T_inner - (T_inner - T_outer) * sum(layers[i][0] for i in range(j+1)) / total_thickness
                   for j in range(3)]
    
    print("初始界面温度估计:", [f"{t:.1f}°C" for t in T_interfaces])
    
    for iter in range(max_iter):
        # 计算各层平均温度和导热系数
        T_avgs = []
        lambdas = []
        R_layers = []
        
        # 第一层：内壁到T2
        T_avg1 = (T_inner + T_interfaces[0]) / 2
        lambda1 = calculate_lambda(T_avg1, layers[0][1], layers[0][2])
        R1 = layers[0][0] / lambda1
        
        # 第二层：T2到T3
        T_avg2 = (T_interfaces[0] + T_interfaces[1]) / 2
        lambda2 = calculate_lambda(T_avg2, layers[1][1], layers[1][2])
        R2 = layers[1][0] / lambda2
        
        # 第三层：T3到T4
        T_avg3 = (T_interfaces[1] + T_interfaces[2]) / 2
        lambda3 = calculate_lambda(T_avg3, layers[2][1], layers[2][2])
        R3 = layers[2][0] / lambda3
        
        # 第四层：T4到外壁
        T_avg4 = (T_interfaces[2] + T_outer) / 2
        lambda4 = calculate_lambda(T_avg4, layers[3][1], layers[3][2])
        R4 = layers[3][0] / lambda4
        
        # 总热阻
        R_total = R1 + R2 + R3 + R4
        q = (T_inner - T_outer) / R_total
        
        # 更新界面温度
        T2_new = T_inner - q * R1
        T3_new = T2_new - q * R2
        T4_new = T3_new - q * R3
        
        # 检查收敛
        diff = max(abs(T2_new - T_interfaces[0]), 
                  abs(T3_new - T_interfaces[1]), 
                  abs(T4_new - T_interfaces[2]))
        
        # 更新界面温度
        T_interfaces = [T2_new, T3_new, T4_new]
        
        print(f"迭代 {iter+1}: q = {q:.2f} W/m², 界面温度: {T2_new:.1f}°C, {T3_new:.1f}°C, {T4_new:.1f}°C")
        
        if diff < tol:
            print(f"收敛于 {iter+1} 次迭代")
            return [lambda1, lambda2, lambda3, lambda4], q, T_interfaces
    
    raise ValueError(f"未在 {max_iter} 次迭代内收敛")

# 输入参数
T_inner = 1100  # 炉内温度 (°C)
T_outer = 65     # 炉外温度 (°C)

# 各层参数 (厚度(m), λ₀(W/m·K), b(K⁻¹))
layers = [
    (0.065, 1.30, 0.0006),    # 耐火砖
    (0.065, 0.15, 0.0003),   # 聚轻球（假设）
    (0.070, 0.08, 0.0001),   # 保温棉
    (0.160, 0.07, 0.0002)    # 保温块（假设）
]

# 运行计算
try:
    lambdas, q, T_interfaces = solve_furnace_wall(T_inner, T_outer, layers)
    
    print("\n=== 最终结果 ===")
    print(f"热流密度 q = {q:.2f} W/m²")
    print("各层导热系数:")
    print(f"  1. 耐火砖: {lambdas[0]:.4f} W/(m·K)  (参考λ₀=1.30)")
    print(f"  2. 聚轻球: {lambdas[1]:.4f} W/(m·K)  (参考λ₀=0.15)")
    print(f"  3. 保温棉: {lambdas[2]:.4f} W/(m·K)  (参考λ₀=0.08)")
    print(f"  4. 保温块: {lambdas[3]:.4f} W/(m·K)  (参考λ₀=0.07)")
    print(f"界面温度: T2={T_interfaces[0]:.1f}°C, T3={T_interfaces[1]:.1f}°C, T4={T_interfaces[2]:.1f}°C")
    
except ValueError as e:
    print(e)

运行结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
初始界面温度估计: ['913.1°C', '726.2°C', '525.0°C']
迭代 1: q = 307.96 W/m², 界面温度: 1090.4°C, 983.3°C, 729.7°C
迭代 2: q = 315.15 W/m², 界面温度: 1090.5°C, 986.3°C, 732.3°C
迭代 3: q = 315.24 W/m², 界面温度: 1090.5°C, 986.3°C, 732.3°C
收敛于 3 次迭代

=== 最终结果 ===
热流密度 q = 315.24 W/m²
各层导热系数:
  1. 耐火砖: 2.1543 W/(m·K)  (参考λ₀=1.30)
  2. 聚轻球: 0.1967 W/(m·K)  (参考λ₀=0.15)
  3. 保温棉: 0.0869 W/(m·K)  (参考λ₀=0.08)
  4. 保温块: 0.0756 W/(m·K)  (参考λ₀=0.07)
界面温度: T2=1090.5°C, T3=986.3°C, T4=732.3°C

结果整理如下：

材料层 厚度(mm) 迭代导热系数λ₀ (W/m·K) 迭代层间温度
耐火砖 65 2.1543 1090.5°C
聚轻球 65 0.1967 986.3°C
保温棉 70 0.0869 732.3°C
保温块 160 0.0756 –

则总热阻为

Rtotal=0.0652.1543+0.0650.1967+0.0700.0869+0.160.0756=3.283m2⋅K/WR_{total}=\frac{0.065}{2.1543}+\frac{0.065}{0.1967}+\frac{0.070}{0.0869}+\frac{0.16}{0.0756}=3.283 m^2\cdot K/W

热流密度为：

q=1100−65Rtotal=315.26W/m2=315.26J/s⋅m−2q=\frac{1100-65}{R_{total}}=315.26 W/m^2 = 315.26 J/s\cdot m^{-2}

则每平方米炉壁每小时散热：

  • 1134.85 kJ/(m²·h)（千焦）
  • 0.3152 kWh/(m²·h)（换算成千瓦时）
  • 0.0317Nm3/(m2⋅h)（换算成标准大气压下天然气消耗(35.8兆焦/方)）

  1. 《传热学》P41 ↩︎